Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm SD, N là trọng tâm tam giác SAB. Đường thẳng MN cắt mặt phẳng (SBC) tại điểm I. Tính tỷ số

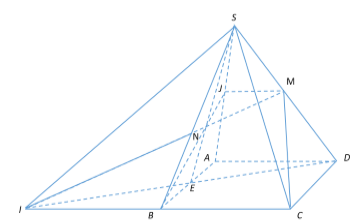
Gọi J;E lần lượt là trung điểm SA;AB.

Trong mặt phẳng (BCMJ) gọi \[I = MN \cap BC\]

Ta có: IM là đường trung tuyến của tam giác SID.

Trong tam giác ICD ta có BE song song và bằng\[\frac{1}{2}CD\] nên suy ra BE là đường trung bình của tam giác ICD⇒EI là trung điểm ID⇒SE là đường trung tuyến của tam giác SID.

Ta có: \[N = IM \cap SE \Rightarrow N\]  là trọng tâm tam giác\[SID \Rightarrow \frac{{IN}}{{IM}} = \frac{2}{3}\]