Cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ các nửa đường thẳng Ax, By, Cz, Dt ở cùng phía so với mặt phẳng (ABCD), song song với nhau và không nằm trong (ABCD). Một mặt ph...

* Hướng dẫn giải

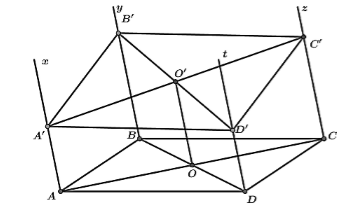
Do (P) cắt mặt phẳng (Ax,By) theo giao tuyến A′B′; cắt mặt phẳng (Cz,Dt) theo giao tuyến C′D′, mà hai mặt phẳng (Ax,By) và (Cz,Dt) song song nên \[A'B'//C'D'\]

Tương tự có \[A'D'//B'C'\] nên A′B′C′D′ là hình bình hành.

Gọi O, O′ lần lượt là tâm ABCD và A′B′C′D′. Dễ dàng có OO′ là đường trung bình của hai hình thang AA′C′C và BB′D′D nên\[OO' = \frac{{AA' + CC'}}{2} = \frac{{BB' + DD'}}{2}\]

Từ đó ta có DD′=2.

 Đáp án cần chọn là: C