Cho tứ diện ABCD có

* Hướng dẫn giải

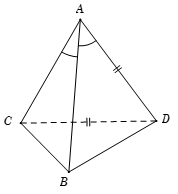
Ta có \[\cos \left( {AB,CD} \right) = \frac{{\left| {\overrightarrow {AB} .\overrightarrow {CD} } \right|}}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {CD} } \right|}} = \frac{{\left| {\overrightarrow {AB} .\overrightarrow {CD} } \right|}}{{AB.CD}}\]

Mặt khác\[\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AB} \left( {\overrightarrow {AD} - \overrightarrow {AC} } \right) = \overrightarrow {AB} .\overrightarrow {AD} - \overrightarrow {AB} .\overrightarrow {AC} \]

\[\begin{array}{*{20}{l}}{ = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AD} } \right|.\cos \left( {\overrightarrow {AB} .\overrightarrow {AD} } \right) - \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} .\overrightarrow {AC} } \right)}\\{ = AB.AD.\cos {{60}^ \circ } - AB.AC.\cos {{60}^ \circ }}\\{ = AB.AD.\frac{1}{2} - AB.\frac{3}{2}AD.\frac{1}{2} = - \frac{1}{4}AB.AD = - \frac{1}{4}AB.CD.}\end{array}\]

Do có\[\cos \left( {AB,CD} \right) = \frac{{\left| { - \frac{1}{4}AB.CD} \right|}}{{AB.CD}} = \frac{1}{4}\]

Vậy\[\cos \varphi = \frac{1}{4}\]

Đáp án cần chọn là: D