Cho hình lập phương ABCD.EFGH. Hãy xác định góc giữa cặp vectơ

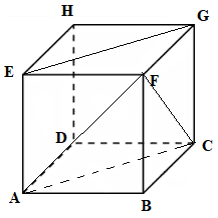
Ta có:

\[\begin{array}{l}\overrightarrow {{\rm{AF}}} = \overrightarrow {AB} + \overrightarrow {AE} \\\overrightarrow {EG} = \overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \end{array}\]

\[ \Rightarrow \overrightarrow {{\rm{AF}}} .\overrightarrow {EG} = \left( {\overrightarrow {AB} + \overrightarrow {AE} } \right).\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) = A{B^2} + \overrightarrow {AE} .\overrightarrow {AB} + \overrightarrow {AB} .\overrightarrow {AD} + \overrightarrow {AE} .\overrightarrow {AD} = A{B^2}\]

\( \Rightarrow \cos \left( {\overrightarrow {AF} ,\overrightarrow {EG} } \right) = \frac{{\overrightarrow {AF} .\overrightarrow {EG} }}{{\left| {\overrightarrow {AF} } \right|.\left| {\overrightarrow {EG} } \right|}} = \frac{{{a^2}}}{{a\sqrt 2 .a\sqrt 2 }} = \frac{1}{2}\)

\( \Rightarrow \widehat {\left( {\overrightarrow {AF} ,\overrightarrow {EG} } \right)} = {60^ \circ }\)