Cho tứ diện ABCD có AB vuông góc với CD, AB=CD=6. M là điểm thuộc cạnh BC sao cho

* Hướng dẫn giải

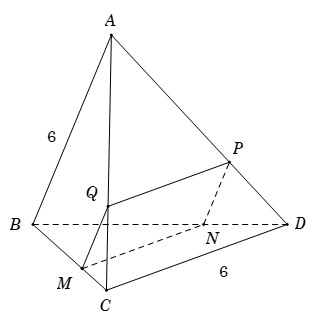
Xét tứ giác MNPQ có\(\left\{ {\begin{array}{*{20}{c}}{MQ//NP//AB}\\{MN//PQ//CD}\end{array}} \right. \Rightarrow MNPQ\) là hình bình hành.

Mặt khác, \[AB \bot CD \Rightarrow MQ \bot MN\] Do đó, MNPQ là hình chữ nhật.

Vì \[MQ//AB\] nên \[\frac{{MQ}}{{AB}} = \frac{{CM}}{{CB}} = x \Rightarrow MQ = x.AB = 6x\]

Theo giả thiết\[MC = x.BC \Rightarrow BM = \left( {1 - x} \right)BC\]

Vì \[MN//CD\] nên\[\frac{{MN}}{{CD}} = \frac{{BM}}{{BC}} = 1 - x \Rightarrow MN = \left( {1 - x} \right).CD = 6\left( {1 - x} \right)\]

Diện tích hình chữ nhật MNPQ là

\[{S_{MNPQ}} = MN.MQ = 6\left( {1 - x} \right).6x = 36.x.\left( {1 - x} \right) \le 36{\left( {\frac{{x + 1 - x}}{2}} \right)^2} = 9\]

Ta có \[{S_{MNPQ}} = 9\] khi\[x = 1 - x \Leftrightarrow x = \frac{1}{2}\]Vậy diện tích tứ giác MNPQ lớn nhất bằng 9 khi M là trung điểm của BC.

Đáp án cần chọn là: A