Trang chủ
Đề thi & kiểm tra
Khác
Góc giữa đường thẳng và mặt phẳng !!
Cho hình chóp S.ABC có đáy ABC là tam giác...
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của gó...
Câu hỏi :
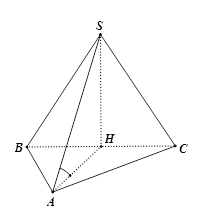
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC).
A.\[{60^0}\]
B. \[{75^0}\]
C. \[{45^0}\]
D. \[{30^0}\]
* Đáp án
* Hướng dẫn giải
Do H là hình chiếu của S lên mặt phẳng (ABC) nên \[SH \bot (ABC)\]
Vậy AH là hình chiếu của SA lên mp (ABC)
\[ \Rightarrow \left( {SA;\left( {ABC} \right)} \right) = \left( {SA;HA} \right) = \widehat {SAH}\] (do\[SH \bot \left( {ABC} \right) \Rightarrow SH \bot AH\]hay \[\widehat {SAH} < {90^0}\]Mà: \[{\rm{\Delta }}ABC = {\rm{\Delta }}SBC \Rightarrow SH = AH\]
Vậy tam giác SAH vuông cân tại H ⇒\[\widehat {SAH} = {45^0}\]
Đáp án cần chọn là: C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Góc giữa đường thẳng và mặt phẳng !!
Số câu hỏi: 16
Copyright © 2021 HOCTAP247
