Trang chủ
Đề thi & kiểm tra
Khác
Góc giữa đường thẳng và mặt phẳng !!
Cho hình chóp S.ABC có đáy ABC là tam giác...
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA=SB=SC=b. Gọi G là trọng tâm
Câu hỏi :
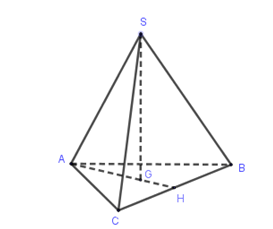
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA=SB=SC=b. Gọi G là trọng tâm \[\Delta ABC\]. Độ dài SG là:
A.\[\frac{{\sqrt {9{b^2} + 3{a^2}} }}{3}\]
B. \[\frac{{\sqrt {{b^2} - 3{a^2}} }}{3}\]
C. \[\frac{{\sqrt {9{b^2} - 3{a^2}} }}{3}\]
D. \[\frac{{\sqrt {{b^2} + 3{a^2}} }}{3}\]
* Đáp án
* Hướng dẫn giải
Theo bài ra hình chóp S.ABC là hình chóp tam giác đều.
Gọi H là trung điểm của BC, ta có\[SG \bot (ABC),G \in AH\]
Mà\[AH = \frac{{a\sqrt 3 }}{2} \Rightarrow AG = \frac{2}{3}AH = \frac{{a\sqrt 3 }}{3}\]
Tam giác SAG vuông tại G nên theo định lý Pi-ta-go ta có :
\[SG = \sqrt {S{A^2} - A{G^2}} = \sqrt {{b^2} - \frac{{{a^2}}}{3}} = \sqrt {\frac{{3{b^2} - {a^2}}}{3}} = \frac{{\sqrt {9{b^2} - 3{a^2}} }}{3}\]
Đáp án cần chọn là: C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Góc giữa đường thẳng và mặt phẳng !!
Số câu hỏi: 16
Copyright © 2021 HOCTAP247
