Cho hình thoi ABCD có tâm

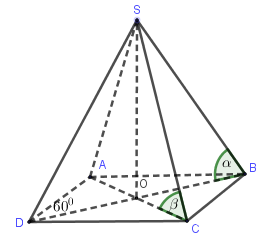
Vì \[SO \bot (ABCD)\;\] nên OB là hình chiếu của SB trên mặt phẳng đáy.

Do đó \[\alpha = \left( {SB,\left( {ABCD} \right)} \right) = \left( {SB,OB} \right) = \widehat {SBO}\] và \[\beta = \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,OC} \right) = \widehat {SCO}\] Hình thoi ABCD có \[AC = 2a,\widehat {ADC} = {60^0} \Rightarrow {\rm{\Delta }}ADC\] đều \[ \Rightarrow AD = 2a\]

Tam giác AOD vuông tại O nên \[OD = \sqrt {A{D^2} - A{O^2}} = \sqrt {4{a^2} - {a^2}} = a\sqrt 3 \Rightarrow OB = a\sqrt 3 \]

Lại có \[\tan \alpha = \frac{1}{2} \Rightarrow \frac{{SO}}{{OB}} = \frac{1}{2} \Rightarrow SO = \frac{1}{2}OB = \frac{1}{2}.a\sqrt 3 = \frac{{a\sqrt 3 }}{2}\] Vậy \[\tan \beta = \tan \widehat {SCO} = \frac{{SO}}{{OC}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{a} = \frac{{\sqrt 3 }}{2}\]