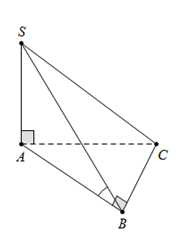
Cho hình chóp S.ABC có đáy ABC. là tam giác vuông tại B, BC=a. Cạnh bên SA=a vuông góc với mặt phẳng đáy. Góc giữa hai mặt phẳng (SBC) và (ABC) bằng

Ta có\[\left( {SBC} \right) \cap \left( {ABC} \right) = BC \Rightarrow BC\]  là giao tuyến.

Mặt khác\[SA \bot \left( {ABC} \right)\] và\[{\rm{\Delta }}ABC\] vuông tại\[B \Rightarrow AB \bot BC\]

Nên \(\left\{ {\begin{array}{*{20}{c}}{SA \bot BC}\\{AB \bot BC}\end{array}} \right. \Rightarrow BC \bot (SAB) \Rightarrow BC \bot SB\)

\(\left\{ {\begin{array}{*{20}{c}}{(SBC) \cap (ABC) = BC}\\{(SBC) \supset SB \bot BC}\\{(ABC) \supset AB \bot BC}\end{array}} \right. \Rightarrow (\widehat {(SBC);(ABC)}) = (\widehat {SB;AB}) = \widehat {SBA} = {45^0}\)

Xét\[\;{\rm{\Delta }}SAB\] vuông tại A, có\[\widehat {SBA} = {45^0} \Rightarrow SA = AB = a\]

Mà\[A{C^2} = A{B^2} + B{C^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 \]