Trang chủ
Đề thi & kiểm tra
Khác
Khoảng cách từ một điểm đến một đường thẳng !!
Cho hình chóp A.BCDcó cạnh
Cho hình chóp A.BCDcó cạnh
Câu hỏi :
Cho hình chóp A.BCDcó cạnh \[AC \bot (BCD)\]và BCD là tam giác đều cạnh bằng a. Biết \(AC = a\sqrt 2 \), khoảng cách từ A đến đường thẳng BD bằng:
A.\[\frac{{3a\sqrt 2 }}{2}\]
B. \[\frac{{2a\sqrt 3 }}{3}\]
C. \[\frac{{4a\sqrt 5 }}{3}\]
D. \[\frac{{a\sqrt {11} }}{2}\]
* Đáp án
* Hướng dẫn giải
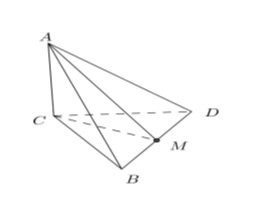
Gọi M là trung điểm của BD.
Ta có: \(\left\{ {\begin{array}{*{20}{c}}{AC \bot BD}\\{CM \bot BD}\end{array}} \right. \Rightarrow BD \bot AM\) (Định lý 3 đường vuông góc)
\[ \Rightarrow d\left( {A;BD} \right) = AM\]
\[CM = \frac{{a\sqrt 3 }}{2}\] (vì tam giác BCD đều).
Ta có: \[AM = \sqrt {A{C^2} + M{C^2}} = \sqrt {2{a^2} + \frac{{3{a^2}}}{4}} = \frac{{a\sqrt {11} }}{2}\]
Đáp án cần chọn là: D
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Khoảng cách từ một điểm đến một đường thẳng !!
Số câu hỏi: 13
Copyright © 2021 HOCTAP247
