Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh aa. Cạnh bên

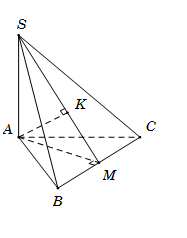
Gọi M là trung điểm BC, suy ra\[AM \bot BC\] và\[AM = \frac{{a\sqrt 3 }}{2}\]

Gọi K là hình chiếu của A trên SM, suy ra \[AK \bot SM\,\,\,\,\,\left( 1 \right)\]

Ta có\(\left\{ {\begin{array}{*{20}{c}}{AM \bot BC}\\{BC \bot SA}\end{array}} \right. \Rightarrow BC \bot (SAM) \Rightarrow BC \bot AK\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)

Từ (1) và (2), suy ra \[AK \bot \left( {SBC} \right)\] nên\[d\left( {A;\left( {SBC} \right)} \right) = AK.\]

Trong\[{\rm{\Delta }}\,SAM\] có \[AK = \frac{{SA.AM}}{{\sqrt {S{A^2} + A{M^2}} }} = \frac{{3a}}{{\sqrt {15} }} = \frac{{a\sqrt {15} }}{5}.\]

Vậy \[d\left( {A;\left( {SBC} \right)} \right) = AK = \frac{{a\sqrt {15} }}{5}.\]