Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Tam giác ABC đều, hình chiếu vuông góc H của đỉnh S trên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Đường thẳng SD...

* Hướng dẫn giải

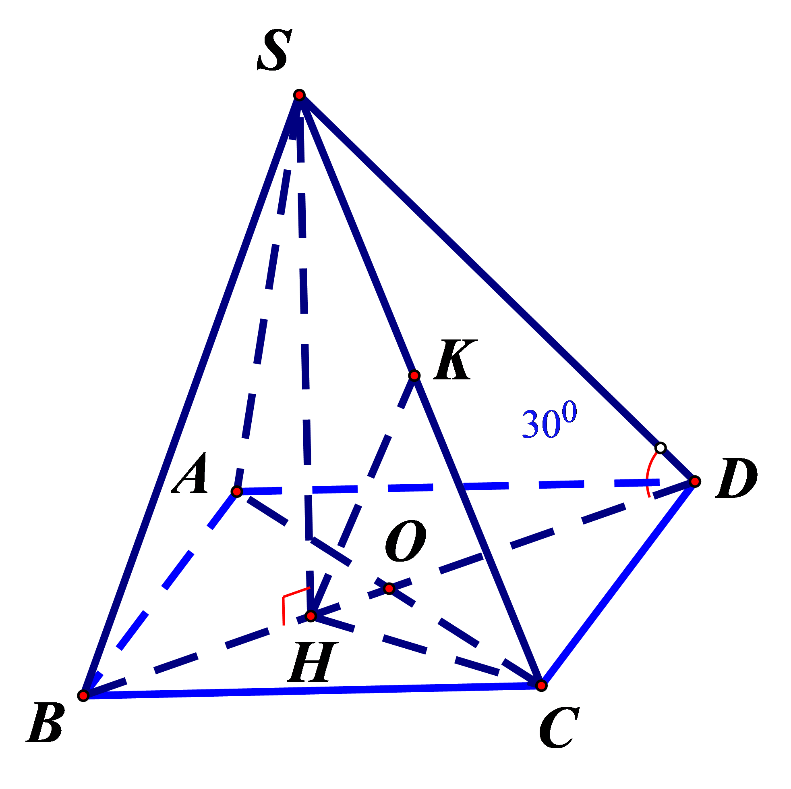
Bước 1: Gọi \[O = AC \cap BD\] Tính BO, CH, HD theo a.

Gọi\[O = AC \cap BD\]

Ta có \[{\rm{\Delta }}ABC\] dều cạnh a có H là trọng tâm

\[ \Rightarrow BO = \frac{{a\sqrt 3 }}{2},CH = \frac{{a\sqrt 3 }}{3},HD = \frac{4}{3}BO = \frac{{2a\sqrt 3 }}{3}\]

Bước 2: Tính SH theo a.

Mặt khác,\[(\widehat {SD,(ABCD)}) = \widehat {SDH} = {30^ \circ }\]

\[ \Rightarrow SH = HD \cdot \tan \widehat {SDH} = \frac{{2a}}{3}\]

Lại có\[CH \bot AB \Rightarrow CH \bot CD\]

Bước 3: Kẻ \[HK \bot SC(K \in SC)\] Chứng minh \[HK \bot CD\]

Kẻ \[HK \bot SC(K \in SC)\]

Ta có:

\(\left\{ {\begin{array}{*{20}{c}}{SH \bot CD}\\{CH \bot CD}\end{array} \Rightarrow CD \bot (SHC) \Rightarrow HK \bot CD \Rightarrow HK \bot (SCD)} \right.\)

Bước 4: Tính\[d\left( {B,\left( {SCD} \right)} \right)\]

\[ \Rightarrow d(H,(SCD)) = HK = \frac{{SH.HC}}{{\sqrt {S{H^2} + H{C^2}} }} = \frac{{2a\sqrt {21} }}{{21}}\]

Mà\[\frac{{d(H,(SCD))}}{{d(B,(SCD))}} = \frac{{HD}}{{BD}} = \frac{2}{3} \Rightarrow d(B,(SCD)) = \frac{{a\sqrt {21} }}{7}\]

Đáp án cần chọn là: C