Nếu gọi ( G 1 ) là đồ thị hàm số y = a^x và ( G 2 ) là đồ thị hàm số y = log a x với 0 < a # 1 . Mệnh đề nào dưới đây đúng ?
Câu hỏi :
Nếu gọi \[({G_1})\]là đồ thị hàm số \[y = {a^x}\;\] và \[({G_2})\]là đồ thị hàm số \[y = lo{g_a}x\;\] với \[0 < a \ne 1\]. Mệnh đề nào dưới đây đúng ?
A.\[({G_1})\]và \[({G_2})\] đối xứng với nhau qua trục hoành.
B. \[({G_1})\]và \[({G_2})\] đối xứng với nhau qua trục tung.
C. \[({G_1})\]và \[({G_2})\] đối xứng với nhau qua đường thẳng y = x.
D. \[({G_1})\]và \[({G_2})\] đối xứng với nhau qua đường thẳng y = −x.
* Đáp án
* Hướng dẫn giải
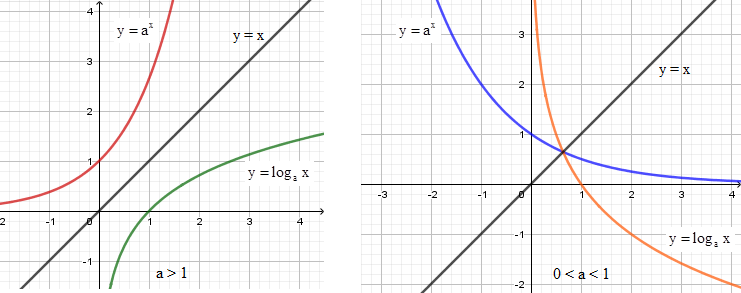
Quan sát hình vẽ ta thấy hai đồ thị hàm số đối xứng nhau qua đường thẳng y=x.
Đáp án cần chọn là: C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Hàm số logarit !!
Số câu hỏi: 30
Copyright © 2021 HOCTAP247
