Số nghiệm của hệ 2^x = 2^y và 2^y = 2^x là:

* Hướng dẫn giải

Trừ phương trình 1 cho 2 vế với vế ta được:

\[{2^x} - {2^y} = 2y - 2x \Leftrightarrow {2^x} + 2x = {2^y} + 2y\]

Xét hàm\[f\left( t \right) = {2^t} + 2t\]có\[f'\left( t \right) = {2^t}\ln 2 + 2 > 0,\forall t \in R\]nên hàm số f(t) đồng biến trên R.

Do đó \[f\left( x \right) = f\left( y \right) \Leftrightarrow x = y\]

Thay y=x vào phương trình\[{2^x} = 2y\]ta được\[{2^x} = 2x \Leftrightarrow {2^x} - 2x = 0\]

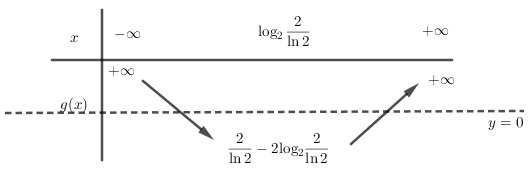
Xét hàm\[y = g\left( x \right) = {2^x} - 2x\]có \[g'\left( x \right) = {2^x}\ln 2 - 2 = 0 \Leftrightarrow x = {\log _2}\frac{2}{{\ln 2}}\]

Suy ra\[g'\left( x \right) > 0 \Leftrightarrow x > {\log _2}\frac{2}{{\ln 2}};g'\left( x \right) < 0 \Leftrightarrow x < {\log _2}\frac{2}{{\ln 2}}\]

\[ \Rightarrow x = {\log _2}\frac{2}{{\ln 2}}\]là điểm cực tiểu của hàm số

\[ \Rightarrow {y_{CT}} = {2^{{{\log }_2}\frac{2}{{\ln 2}}}} - 2{\log _2}\frac{2}{{\ln 2}} = \frac{2}{{\ln 2}} - 2{\log _2}\frac{2}{{\ln 2}} < 0\]

Mặt khác\[\mathop {\lim }\limits_{x \to \pm \infty } g(x) = + \infty \]suy ra đường thẳng y=0 cắt đồ thị hàm số y=g(x) tại 2 điểm phân biệt.

Vậy số nghiệm của hệ là 2

Đáp án cần chọn là: A