Cho hàm số y = x^4 − 2 m x^2 + m^2 + m . . Tất cả các giá trị của m để đồ thị hàm số có 3 điểm cực trị tạo thành tam giác có một góc 120o là:

\[\begin{array}{l}y\prime = 4{x^3} - 4mx\\y\prime = 0 \Leftrightarrow 4{x^3} - 4mx = 0 \Leftrightarrow 4x({x^2} - m) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x = \pm \sqrt m }\end{array}} \right.\end{array}\]

Điều kiện để hàm số có 3 cực trị: m>0

\[\begin{array}{*{20}{l}}{x = 0 \Rightarrow A\left( {0;\,{m^2} + m} \right)}\\{x = - \sqrt m \Rightarrow y = {{\left( { - \sqrt m } \right)}^4} - 2m{{\left( { - \sqrt m } \right)}^2} + {m^2} + m}\\{ = {m^2} - 2{m^2} + {m^2} + m = m \Rightarrow B\left( { - \sqrt m ;\,m} \right)}\\{x = \sqrt m \Rightarrow C\left( {\sqrt m ;\,m} \right)}\end{array}\]

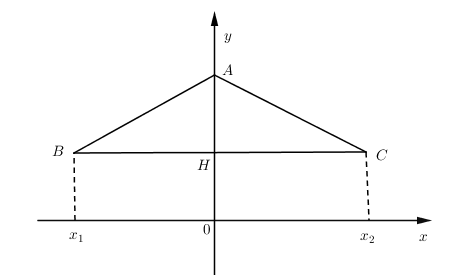
\[\begin{array}{l}\overrightarrow {AB} = ( - \sqrt m ; - {m^2}),\overrightarrow {AC} = (\sqrt m ; - {m^2})\\\widehat {BAC} = {120^0}\end{array}\]

\(\begin{array}{l} \Leftrightarrow \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = cos{120^0}\\ \Leftrightarrow \frac{{ - m + {m^4}}}{{\sqrt {m + {m^4}} .\sqrt {m + {m^4}} }} = - \frac{1}{2}\\ \Leftrightarrow 2({m^4} - m) = - (m + {m^4})\\ \Leftrightarrow 3{m^4} - m = 0\\ \Leftrightarrow m(3{m^3} - 1) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 0(loai)}\\{m = \frac{1}{{\sqrt[3]{3}}}}\end{array}} \right.\end{array}\)