Cho hàm số y=f(x) liên tục trên

* Hướng dẫn giải

Ta có \[g\left( x \right) = 2f\left( x \right) - {x^2} \Rightarrow g'\left( x \right) = 2f'\left( x \right) - 2x\]

Cho\[g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = x\,\,\,\left( 1 \right)\]

Nghiệm của phương trình (1) là hoành độ giao điểm của hai đồ thị hàm số

\[y = f'\left( x \right);\,\,y = x.\]

Vẽ đường thẳng y=xy=x và đồ thị hàm số \[y = f'\left( x \right)\] trên cùng hệ trục tọa độ:

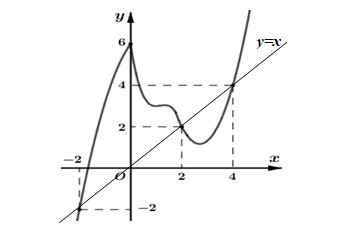
Dựa vào đồ thị ta thấy đồ thị hai hàm số\[y = f'\left( x \right);\,\,y = x\] cắt nhau tại 3 điểm có hoành độ là \[ - 2;2;4.\]

\[ \Rightarrow g\prime (x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = - 2}\\{x = 2}\\{x = 4}\end{array}} \right.\]Bảng biến thiên đồ thị hàm số\[y = g\left( x \right)\]

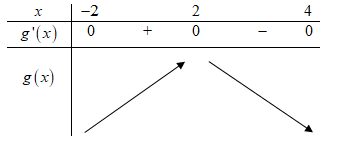
Dựa vào bảng biến thiên ta thấy giá trị lớn nhất của hàm số g(x) trên đoạn \[\left[ { - 2;4} \right]\;\]là g(2).

Đáp án cần chọn là: B