Khi xây nhà, cô Ngọc cần xây một bể đựng nước mưa có thể tích V=6m3 dạng hình hộp chữ nhật với chiều dài gấp ba lần chiều rộng, đáy và nắp và các mặt xung quanh đều được đổ bê tông...

* Hướng dẫn giải

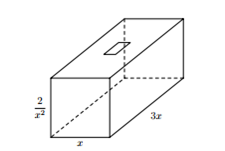
Bước 1: Gọi x(m),3x(m) lần lượt là chiều rộng, chiều dài của bể. Tính chiều cao của bể.

Gọi x(m),3x(m) lần lượt là chiều rộng, chiều dài của bể, h là chiều cao của bể.

Theo bài ra ta có: \[V = x.3x.h = 6 \Rightarrow h = \frac{6}{{3{x^2}}} = \frac{2}{{{x^2}}}\,\,\left( m \right)\]

Bước 2: Tính tổng diện tích các mặt làm bê tông.

Khi đó tổng diện tích các mặt bể được làm bê tông là:

\[2x.\frac{2}{{{x^2}}} + 2.3x.\frac{2}{{{x^2}}} + 2x.3x - x.3x.\frac{2}{9} = \frac{{16{x^2}}}{3} + \frac{{16}}{x}\]

Bước 3: Sử dụng BĐT Cô-si cho 3 số dương để tính số tiền ít nhất cần tìm

Áp dụng BĐT Cô-si ta có:

\[\frac{{16{x^2}}}{3} + \frac{{16}}{x} = \frac{{16{x^2}}}{3} + \frac{8}{x} + \frac{8}{x} \ge 3\sqrt[3]{{\frac{{16{x^2}}}{3}.\frac{8}{x}.\frac{8}{x}}} = 8\sqrt[3]{{18}}\]

Dấu “=” xảy ra khi\[\frac{{16{x^2}}}{3} = \frac{8}{x} \Leftrightarrow x = \sqrt[3]{{\frac{3}{2}}}\]

Vậy số tiền ít nhất mà cô Ngọc cần bỏ ra là \[8\sqrt[3]{{18}}{.10^6} \approx 21.000.000d\]