Tích phân I = nguyên hàm từ pi/3 đến pi/2 dx/sin x có giá trị bằng

Cách 1:

\[\begin{array}{l}I = \mathop \smallint \limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} \frac{{dx}}{{\sin x}}\\ = \mathop \smallint \limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} \frac{{\left( {co{s^2}\frac{x}{2} + si{n^2}\frac{x}{2}} \right)}}{{2sin\frac{x}{2}cos\frac{x}{2}}}dx\\ = \frac{1}{2}\mathop \smallint \limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} \left( {cot\frac{x}{2} + tan\frac{x}{2}} \right)dx\\ = \left[ {\ln \left| {sin\frac{x}{2}} \right| - \ln \left| {cos\frac{x}{2}} \right|} \right]\left| {_{\frac{\pi }{3}}^{\frac{\pi }{2}}} \right.\\ = \left[ {\ln \frac{{\sqrt 2 }}{2} - \ln \frac{{\sqrt 2 }}{2}} \right] - \left[ {\ln \frac{1}{2} - \ln \frac{{\sqrt 3 }}{2}} \right]\\ = \ln \sqrt 3 \end{array}\]

Cách 2:

Bước 1: Dùng máy tính như hình dưới, thu được giá trị 0,549306...

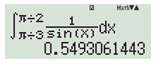
Bước 2: Lấy\[{e^{0,549306...}}\]cho kết quả \[1,732050808... \approx \sqrt 3 \]Chọn\[\frac{1}{2}\ln 3\]

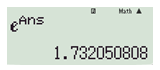
Cách 3:

Thực hiện các phép tính sau trên máy tính (đến khi thu được kết quả bằng 0 thì ngưng)

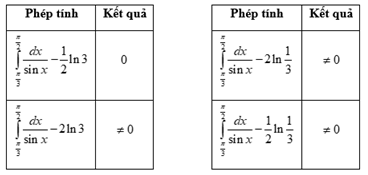
Chọn \[\frac{1}{2}\ln 3\]