Cho hình lăng trụ ABCD.A′B′C′D′ có đáy ABCD là hình chữ nhật với

* Hướng dẫn giải

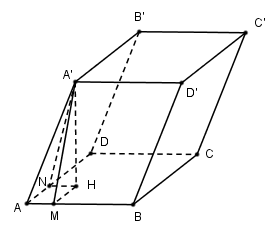
Kẻ\[A'H \bot \left( {ABCD} \right);HM \bot AB;HN \bot AD\]

Ta có:\(\left. {\begin{array}{*{20}{c}}{A\prime H \bot AB}\\{HM \bot AB}\end{array}} \right\} \Rightarrow AB \bot (A\prime HM) \Rightarrow AB \bot A\prime M\)

\(\left. {\begin{array}{*{20}{c}}{(ABB\prime A\prime ) \cap (ABCD) = AB}\\{(ABB\prime A\prime ) \supset A\prime M \bot AB}\\{(ABCD) \supset HM \bot AB}\end{array}} \right\} \Rightarrow ((ABB\prime \widehat {A\prime );(A}BCD)) = (A\prime \widehat {M;H}M) = \widehat {A\prime MH} = {45^o}\)

Chứng minh tương tự ta có\[\widehat {A'NH} = {60^0}\]

Đặt A′H=x khi đó ta có:

\[A'N = \frac{x}{{\sin 60}} = \frac{{2x}}{{\sqrt 3 }},AN = \sqrt {A{A^{\prime 2}} - A'{N^2}} = \sqrt {1 - \frac{{4{x^2}}}{3}} = HM\]

Mà \[HM = x.\cot 45 = x\]

\[ \Rightarrow x = \sqrt {1 - \frac{{4{x^2}}}{3}} \Leftrightarrow {x^2} = 1 - \frac{{4{x^2}}}{3} \Leftrightarrow \frac{{7{x^2}}}{3} = 1 \Rightarrow {x^2} = \frac{3}{7} \Rightarrow x = \sqrt {\frac{3}{7}} \]

\[{S_{ABCD}} = \sqrt 3 .\sqrt 7 = \sqrt {21} \]Vậy\[{V_{ABCD.A'B'C'D'}} = A'H.{S_{ABCD}} = \sqrt {\frac{3}{7}} .\sqrt {21} = 3\]

Đáp án cần chọn là: A