Cho hình lăng trụ xiên ABC.A′B′C′ có đáy ABC là tam giác đều với tâm O. Hình chiếu của C′ trên (ABC) là O. Tính thể tích của lăng trụ biết rằng khoảng cách từ O đến CC′ là a và 2 m...

* Hướng dẫn giải

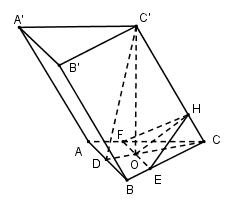
Gọi D là trung điểm của AB. Trong (CC′D) kẻ \[OH \bot CC' \Rightarrow OH = a\]

\(\left. {\begin{array}{*{20}{c}}{CD \bot AB}\\{C\prime O \bot AB}\end{array}} \right\} \Rightarrow AB \bot (CC\prime D) \Rightarrow AB \bot CC\prime \)

Trong (ABC), qua O kẻ\[EF//AB\left( {E \in BC;F \in AC} \right)\]

Ta có: \(\left. {\begin{array}{*{20}{c}}{EF \bot CC\prime }\\{OH \bot CC'}\end{array}} \right\} \Rightarrow CC\prime \bot (EFH) \Rightarrow CC\prime \bot HE;CC\prime \bot HF\)

Ta có:

\(\left. {\begin{array}{*{20}{c}}{(ACC\prime A\prime ) \cap (BCC\prime B\prime ) = CC\prime }\\{(ACC\prime A\prime ) \supset HF \bot CC\prime }\\{(BCC\prime B\prime ) \supset HE \bot CC\prime }\end{array}} \right\} \Rightarrow ((ACC\prime \widehat {A\prime );(B}CC\prime B\prime )) = (H\widehat {F;H}E) = {90^0}\)

\[ \Rightarrow HE \bot HF\]

\[ \Rightarrow {\rm{\Delta }}HEF\] vuông tại H

\[{\rm{\Delta }}HCE = {\rm{\Delta }}HCF\left( {c.g.v - c.h} \right) \Rightarrow HE = HF \Rightarrow {\rm{\Delta }}HEF\] vuông cân tại H\[ \Rightarrow EF = 2HO = 2a\]

Ta có:\[\frac{{EF}}{{AB}} = \frac{{CO}}{{CD}} = \frac{2}{3} \Rightarrow AB = \frac{3}{2}EF = \frac{3}{2}.2a = 3a\]

\[ \Rightarrow {S_{{\rm{\Delta }}ABC}} = \frac{{A{B^2}\sqrt 3 }}{4} = \frac{{9{a^2}\sqrt 3 }}{4}\]

\[CD = \frac{{AB\sqrt 3 }}{2} = \frac{{3a\sqrt 3 }}{2} \Rightarrow CO = \frac{2}{3}AB = \frac{2}{3}.\frac{{3a\sqrt 3 }}{2} = a\sqrt 3 \]

\[C'O \bot \left( {ABC} \right) \Rightarrow C'O \bot CO \Rightarrow {\rm{\Delta }}CC'O\] vuông tại O

\[ \Rightarrow \frac{1}{{O{H^2}}} = \frac{1}{{C'{O^2}}} + \frac{1}{{C{O^2}}} \Rightarrow \frac{1}{{C'{O^2}}} = \frac{1}{{O{H^2}}} - \frac{1}{{C{O^2}}} = \frac{1}{{{a^2}}} - \frac{1}{{3{a^2}}} = \frac{2}{{3{a^2}}} \Rightarrow C'O = \frac{{\sqrt 6 }}{2}a\]

Vậy\[{V_{ABC.A'B'C'}} = C'O.{S_{{\rm{\Delta }}ABC}} = \frac{{a\sqrt 6 }}{2}.\frac{{9{a^2}\sqrt 3 }}{4} = \frac{{27{a^3}\sqrt 2 }}{8}\]

Đáp án cần chọn là: D