Cho hình lăng trụ đứng ABC.A′B′C′ có đáy là tam giác cân tại A.

* Hướng dẫn giải

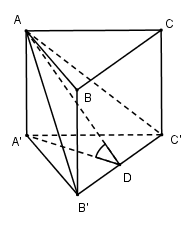
Gọi D là trung điểm của B′C′. Vì tam giác A′B′C′ cân tại A′  nên \[A'D \bot B'C'\] (trung tuyến đồng thời là đường cao).

Vì ABC.A′B′C′ là hình lăng trụ đứng nên\[AA' \bot (A'B'C')\]

Ta có:\(\left. {\begin{array}{*{20}{c}}{A\prime D \bot B\prime C\prime }\\{AA\prime \bot B\prime C\prime }\end{array}} \right\} \Rightarrow B\prime C\prime \bot (AA\prime D) \Rightarrow B\prime C\prime \bot AD\)

\(\left. {\begin{array}{*{20}{c}}{(AB\prime C\prime ) \cap (A\prime B\prime C\prime ) = B\prime C'}\\{(AB\prime C\prime ) \supset AD \bot B\prime C\prime }\\{(A\prime B\prime C\prime ) \supset A\prime D \bot B\prime C\prime }\end{array}} \right\} \Rightarrow ((AB\prime \widehat {C\prime );(A\prime }B\prime C\prime )) = (A\widehat {D;A\prime }D) = \widehat {ADA}\prime = {60^0}\)

Vì tam giác A′B′C′ cân tại A′  nên\[\widehat {DA'C'} = \frac{1}{2}\widehat {B'A'C'} = {60^0}\] (trung tuyến đồng thời là phân giác)

Xét tam giác vuông A′D′C′ có: \[A'D = A'C'.cos60 = 2a.\frac{1}{2} = a\]

Xét tam giác vuông AA′D có:\[AA' = A'D.\tan 60 = a.\sqrt 3 \]

\[{S_{ABC}} = \frac{1}{2}AB.AC.\sin \widehat {BAC} = \frac{1}{2}.2a.2a.\frac{{\sqrt 3 }}{2} = {a^2}\sqrt 3 \]

Vậy\[{V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = a\sqrt 3 .{a^2}\sqrt 3 = 3{a^3}\]

Đáp án cần chọn là: D