Đề thi THPT QG - 2021 - mã 101Cho khối hộp chữ nhật ABCD.A′B′C′D′ có đáy là hình vuông, BD=2a, góc giữa hai mặt phẳng [(A prime BD) ; ]và (ABCD) bằng 300. Thể tích của khối hộp chữ...

* Hướng dẫn giải

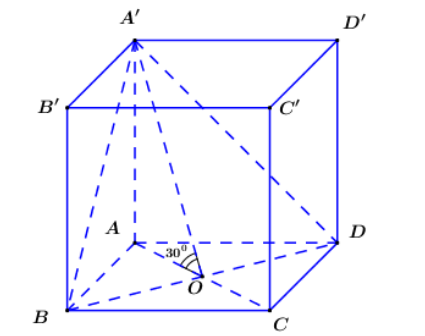
* Xác định\[\angle \left( {\left( {A'BD} \right);\left( {ABCD} \right)} \right)\]

+\[\left( {A'BC} \right) \cap \left( {ABCD} \right) = BD\]

+\(\left\{ {\begin{array}{*{20}{c}}{AA\prime \bot BD}\\{AO \bot BD}\end{array}} \right. \Rightarrow (A\prime AO) \bot BD\)

+ \(\left\{ {\begin{array}{*{20}{c}}{(A\prime AO) \cap (A\prime BD) = A\prime O}\\{(A\prime AO) \cap (ABCD) = AO}\end{array}} \right.\)

\[ \Rightarrow \angle \left( {\left( {A'BD} \right);\left( {ABCD} \right)} \right) = \angle \left( {A'O;AO} \right) = \angle A'OA\]

\[ \Rightarrow \angle A'OA = {30^0}\]

* Xét tam giác A′OA vuông tại A có\[AO = \frac{1}{2}AC = \frac{1}{2}BD = a\]

\[ \Rightarrow AA' = \tan {30^0}.AO = \frac{{a\sqrt 3 }}{3}\]

\[ \Rightarrow {V_{ABCD.A'B'C'D'}} = {S_{ABCD}}.AA' = \frac{1}{2}AC.BD.AA'\]

\[ = \frac{1}{2}.{\left( {2a} \right)^2}.\frac{{a\sqrt 3 }}{3} = \frac{{2\sqrt 3 {a^3}}}{3}\]

Đáp án cần chọn là: D