Trang chủ
Đề thi & kiểm tra
Khác
Diện tích hình nón, thể tích khối nón !!
Cho hình nón đỉnh S, tâm đáy là O, góc...
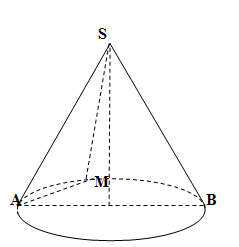
Cho hình nón đỉnh S, tâm đáy là O, góc ở đỉnh là 1350. Trên đường tròn đáy lấy điểm A cố định và điểm M di động. Tìm số vị trí M để diện tích SAM đạt giá trị lớn nhất
Câu hỏi :
Cho hình nón đỉnh S, tâm đáy là O, góc ở đỉnh là 1350. Trên đường tròn đáy lấy điểm A cố định và điểm M di động. Tìm số vị trí M để diện tích SAM đạt giá trị lớn nhất
A.Vô số
B.3
C.2
D.1
* Đáp án
* Hướng dẫn giải
Ta có:
\[\begin{array}{*{20}{l}}{{S_{SAM}} = \frac{1}{2}SA.SM\sin \widehat {ASM}}\\{ = \frac{1}{2}S{A^2}\sin \widehat {ASM} \le \frac{1}{2}S{A^2}}\\{ \Rightarrow \max {S_{SAM}} = \frac{1}{2}S{A^2}}\end{array}\]
Dấu “=” xảy ra khi \[\sin \widehat {ASM} = 1 \Leftrightarrow \widehat {ASM} = {90^0}\]
Có 2 điểm M như vậy (hai điểm đối xứng với nhau qua AB).
Đáp án cần chọn là: C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Diện tích hình nón, thể tích khối nón !!
Số câu hỏi: 28
Copyright © 2021 HOCTAP247
