Cho hình vuông ABCD cạnh bằng 2. Gọi M là trung điểm AB. Cho tứ giác AMCD và các điểm trong của nó quay quanh trục AD ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.

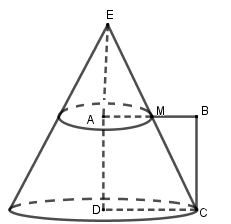
Kéo dài CM cắt DA tại E. Quay hình thang vuông AMCD quanh trục AD ta được hình nón cụt như hình vẽ.

Quay tam giác EDC quanh trục ED ta được hình nón.

Dễ thấy \[{V_{nc}} = {V_1} - {V_2}\] V1V1 là thể tích khối nón đỉnh E, bán kính đáy DC = 2DC = 2 và V2 là thể tích khối nón đỉnh E, bán kính đáy AM = 1

Có\[\frac{{EA}}{{ED}} = \frac{{AM}}{{DC}} = \frac{1}{2} \Rightarrow EA = AD = 2 \Rightarrow ED = 4\]

\[ \Rightarrow {V_1} = \frac{1}{3}\pi D{C^2}.ED = \frac{1}{3}\pi {.2^2}.4 = \frac{{16\pi }}{3}\]

\[{V_2} = \frac{1}{3}\pi A{M^2}EA = \frac{1}{3}\pi {.1^2}.2 = \frac{{2\pi }}{3}\]

Vậy \[V = {V_1} - {V_2} = \frac{{16\pi }}{3} - \frac{{2\pi }}{3} = \frac{{14\pi }}{3}\]