Khẳng định nào sau đây là đúng? A. y = |tanx| đồng biến trong [- pi/2; pi/2]
Câu hỏi :
Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?
A. y = |tanx| đồng biến trong
B. y = |tanx| là hàm số chẵn trên D = R\
C. y = |tanx| có đồ thị đối xứng qua gốc tọa độ.
D. y = |tanx| luôn nghịch biến trong
* Đáp án
* Hướng dẫn giải
Ta có đồ thị hàm số y = |tanx| như sau:
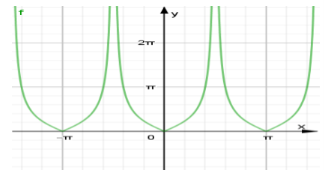
TXĐ: D = R\
Dựa vào đồ thị hàm số ta thấy:
- Hàm số y = |tanx| nghịch biến trên và đồng biến trên ,do đó đáp án A và D sai.
- Đặt f(x) = |tanx|, ∀x∈D ⇒ −x∈D
f(−x) = |tan(−x)| = |−tanx| = |tanx| = f(x), do đó hàm số đã cho là hàm chẵn trên tập xác định. Do đó đáp án B đúng.
- Do là hàm chẵn nên đồ thị hàm số đối xứng qua trục Oy chứ không đối xứng qua tâm O, do đó đáp án C sai.
Đáp án cần chọn là: B
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Các hàm số lượng giác !!
Số câu hỏi: 28
Copyright © 2021 HOCTAP247
