Tìm m để hàm số y = căn bậc hai (8cosx - 6sinx - (3sinx - 4cosx)^2 - 2m) có tập xác định là R.
Câu hỏi :
Tìm m để hàm số có tập xác định là R.
Tìm m để hàm số có tập xác định là R.
A.
B.
C.
D.
* Đáp án
* Hướng dẫn giải
Bước 1:
Ta có:
Hàm số trên có tập xác định R khi:
Bước 2:
Đặt t = 4cosx − 3sinx
Theo BĐT Bu-nhi-a-cốp-xki ta có:
Bước 3:
Ta có bất phương trình
Bước 4:
Xét hàm số f(t) = t2 − 2t trên [−5; 5]
Ta có
Vì a = 1 > 0 nên hàm số nghịch biến trên (−∞;1) và đồng biến trên (1;+∞)
Mà (−5;1)⊂(−∞;1) và (1;5)⊂(1;+∞) nên hàm số nghịch biến trên (−5;1) và đồng biến trên (1;5).
Bảng biến thiên:
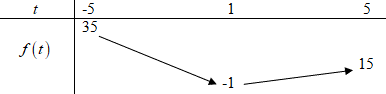
Bước 5:
Dựa vào bảng biến thiên ta thấy bất đẳng thức (1) xảy ra khi
Đáp án cần chọn là: A
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Các hàm số lượng giác !!
Số câu hỏi: 28
Copyright © 2021 HOCTAP247
