Trang chủ
Đề thi & kiểm tra
Khác
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số !!
Một sợi dây kim loại dài a(cm) . Người ta...
Một sợi dây kim loại dài a(cm) . Người ta cắt sợi dây đó thành hai đoạn, trong đó một đoạn có độ dài x(cm)
Câu hỏi :
Một sợi dây kim loại dài a(cm) . Người ta cắt sợi dây đó thành hai đoạn, trong đó một đoạn có độ dài x(cm) được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông Tìm x để hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất.
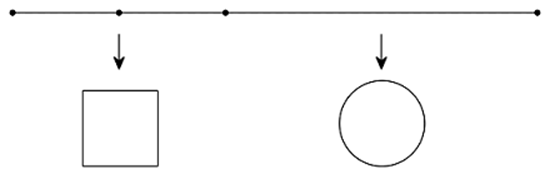
Một sợi dây kim loại dài a(cm) . Người ta cắt sợi dây đó thành hai đoạn, trong đó một đoạn có độ dài x(cm) được uốn thành đường tròn và đoạn còn lại được uốn thành hình vuông Tìm x để hình vuông và hình tròn tương ứng có tổng diện tích nhỏ nhất.

A.
B.
C.
D.
* Đáp án
* Hướng dẫn giải
Do x là độ dài của đoạn dây cuộn thành hình tròn Suy ra chiều dài đoạn còn lại là a − x.
Gọi r là bán kính của đường tròn. Chu vi đường tròn:
Do đó diện tích hình tròn là:
Chu vi hình vuông là Cạnh hình vuông là Do đó diện tích hình vuông:
Tổng diện tích hai hình:
Xét hàm số ta có:
Cho Ta có BBT như sau :
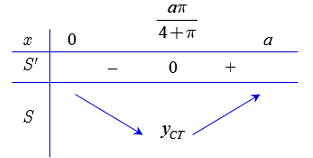
Suy ra hàm S chỉ có một cực trị và là cực tiểu tại
Do đó S đạt giá trị nhỏ nhất tại
Đáp án cần chọn là: C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số !!
Số câu hỏi: 42
Copyright © 2021 HOCTAP247
