Trang chủ
Đề thi & kiểm tra
Khác
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số !!
Cho hàm số y = f(x) có đạo hàm trên...
Cho hàm số y = f(x) có đạo hàm trên và có đồ thị như hình vẽ bên. Xét hàm số g(x) = f(x^3 + 2x) + m
Câu hỏi :
Cho hàm số có đạo hàm trên và có đồ thị như hình vẽ bên. Xét hàm số . Giá trị của tham số m để giá trị lớn nhất của hàm số g(x) trên đoạn bằng 9 là:
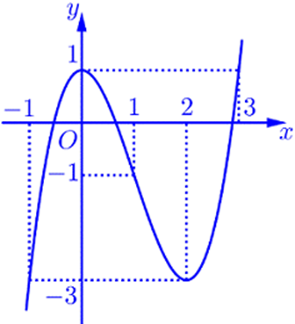
Cho hàm số có đạo hàm trên và có đồ thị như hình vẽ bên. Xét hàm số . Giá trị của tham số m để giá trị lớn nhất của hàm số g(x) trên đoạn bằng 9 là:

A.m=10
B.m=6
C.m=12
D.m=8
* Đáp án
* Hướng dẫn giải
Ta có :
(Do phương trình vô nghiệm).
Từ đồ thị hàm số f(x) đã cho ta có
Hàm số g(x) trên đoạn có :
Do đó,
Theo giả thiết, giá trị lớn nhất của hàm số g(x) trên bằng 9 nên
Vậy m = 8.
Đáp án cần chọn là: D
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số !!
Số câu hỏi: 42
Copyright © 2021 HOCTAP247
