Trang chủ
Đề thi & kiểm tra
Khác
Đường tiệm cận của đồ thị hàm số !!
Cho hàm số f(x)=ax^3+bx^2+cx+d có đồ thị như hình vẽ...
Cho hàm số f(x)=ax^3+bx^2+cx+d có đồ thị như hình vẽ bên: Hỏi đồ thị hàm số g(x)=(x^2-3x+2)căn bậc hai (x-1)/x[f^2(x)-f(x)]
Câu hỏi :
Cho hàm số có đồ thị như hình vẽ bên.
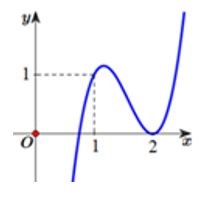
Hỏi đồ thị hàm số có bao nhiêu tiệm cận đứng?
Cho hàm số có đồ thị như hình vẽ bên.

Hỏi đồ thị hàm số có bao nhiêu tiệm cận đứng?
A.4
B.3
C.5
D.2
* Đáp án
* Hướng dẫn giải
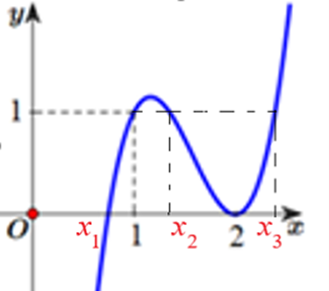
ĐKXĐ:
Nhận xét: là hàm số bậc ba, đồng thời, quan sát đồ thị ta thấy:
có 2 nghiệm phân biệt (nghiệm đơn) và x = 2(nghiệm kép).
+) có 3 nghiệm phân biệt x = 1 (nghiệm đơn), (nghiệm đơn) và (nghiệm đơn).
Khi đó hàm số được viết dưới dạng :
Do đó, đồ thị hàm số g(x) có 3 đường tiệm cận đứng là:
Đáp án cần chọn là: B
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đường tiệm cận của đồ thị hàm số !!
Số câu hỏi: 25
Copyright © 2021 HOCTAP247
