Trang chủ
Đề thi & kiểm tra
Khác
Bài toán tương giao đồ thị !!
Cho hàm số y = f(x) =ax^3 + bx^2 +...
Cho hàm số y = f(x) =ax^3 + bx^2 + cx + d có đồ thị như hình dưới đây. Có tất cả bao nhiêu giá trị nguyên
Câu hỏi :
Cho hàm số có đồ thị như hình dưới đây
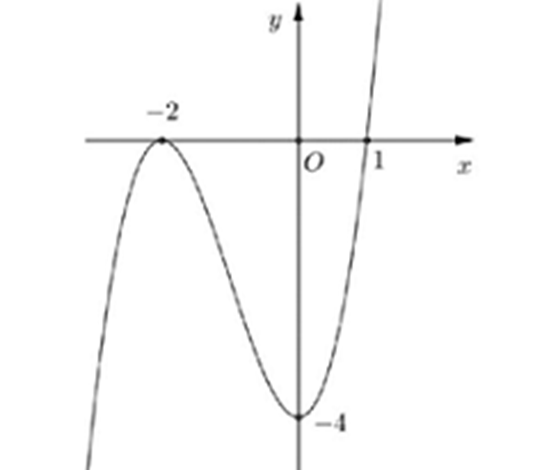
Có tất cả bao nhiêu giá trị nguyên của tham số để phương trình có 6 nghiệm phân biệt

Có tất cả bao nhiêu giá trị nguyên của tham số để phương trình có 6 nghiệm phân biệt
A.2.
B.4.
C.3.
D.5.
* Đáp án
* Hướng dẫn giải
Ta có
Dựng đồ thị hàm số ta được:
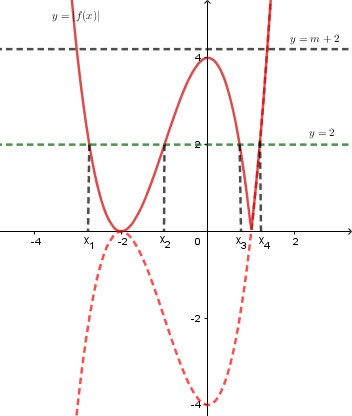
Dễ thấy phương trình có 4 nghiệm phân biệt nên để phương trình đã cho có 6 nghiệm phân biệt thì phương trình phải có 2 nghiệm phân biệt khác các nghiệm trên.
Do đó đường thẳng cắt đồ thị hàm số tại 2 điểm phân biệt.
Từ hình vẽ ta có
Mà và nên
Vậy có 3 giá trị thỏa mãn.
Đáp án cần chọn là: C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài toán tương giao đồ thị !!
Số câu hỏi: 33
Copyright © 2021 HOCTAP247
