Trang chủ
Đề thi & kiểm tra
Khác
Sự đồng biến, nghịch biến của hàm số !!
Cho hàm số y = f(x) liên tục trên R...
Cho hàm số y = f(x) liên tục trên R và có đạo hàm f'(x) = x^2(x - 2)(x^2 - 6x + m) với mọi x thuộc R
Câu hỏi :
Cho hàm số liên tục trên và có đạo hàm với mọi . Có bao nhiêu số nguyên m thuộc đoạn để hàm số nghịch biến trên khoảng
Cho hàm số liên tục trên và có đạo hàm với mọi . Có bao nhiêu số nguyên m thuộc đoạn để hàm số nghịch biến trên khoảng
A.2010.
B.2012.
C.2011.
D.2009.
* Đáp án
* Hướng dẫn giải
Ta có:
Hàm số g(x) nghịch biến trên
(do
Ta có:
BBT:
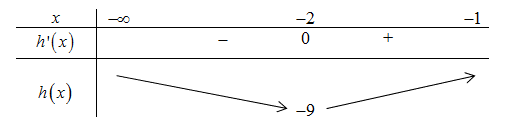
Dựa vào BBT ta có
Mà và m nguyên nên hay
có giá trị của m thỏa mãn.
Đáp án cần chọn là: C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Sự đồng biến, nghịch biến của hàm số !!
Số câu hỏi: 22
Copyright © 2021 HOCTAP247
