Trang chủ Đề thi & kiểm tra Khác Sự đồng biến, nghịch biến của hàm số !! Cho hàm số đa thức f(x) có đạo hàm tràm...

Cho hàm số đa thức f(x) có đạo hàm tràm trên R. Biết f(0)=0 và đồ thị hàm số y = f'(x) như hình sau

Câu hỏi :

Cho hàm số đa thức f(x) có đạo hàm tràm trên R. Biết f0=0  và đồ thị hàm số y=f'(x)  như hình sau.

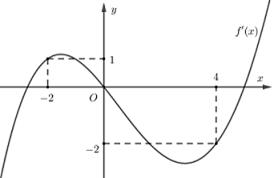
Media VietJack

Hàm số gx=4fx+x2  đồng biến trên khoảng nào dưới đây ?

A. 4;+∞


B.(0;4).


C.−∞;−2


D.(−2;0).


* Đáp án

* Hướng dẫn giải

Đặt hx=4fx+x2 ta có h'x=4fx+2x=4f'x+x2

Số nghiệm của phương trình h'(x)=0   là số giao điểm của đồ thị hàm số y=f'(x) và đường thẳng y=−x2 .

Vẽ đồ thị hàm số y=f'(x) và đường thẳng y=−x2 trên cùng mặt phẳng tọa độ ta có:

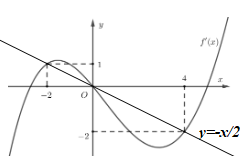
Media VietJack

Dựa vào đồ thị hàm số ta thấy  h'(x)=0⇔x=−2x=0x=4

Khi đó ta có BBT hàm số y=h(x) :

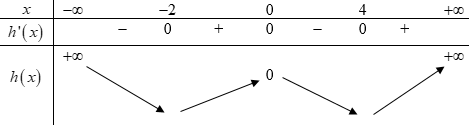
Media VietJack

Khi đó ta suy ra được BBT hàm số gx=hx như sau:

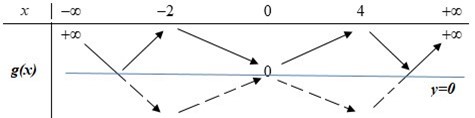
Media VietJack

Dựa vào BBT và các đáp án ta thấy hàm số g(x) đồng biến trên (0;4)

Đáp án cần chọn là: B

Câu hỏi trên thuộc đề trắc nghiệm dưới đây !

Sự đồng biến, nghịch biến của hàm số !!

Số câu hỏi: 22

Khác

Home
Tiểu học Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Hóa học Tài liệu Đề thi & kiểm tra Câu hỏi hoctapsgk.com Nghe truyện audio Đọc truyện chữ Công thức nấu ăn

Copyright © 2021 HOCTAP247