Cho hàm số y = f(x) có đạo hàm liên tục trên R và đồ thị hàm số y = f(x) như hình vẽ bên. Tìm số điểm cực trị
Câu hỏi :
Cho hàm số có đạo hàm liên tục trên và đồ thị hàm số như hình vẽ bên. Tìm số điểm cực trị của hàm số
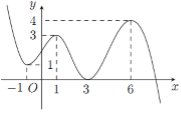
Cho hàm số có đạo hàm liên tục trên và đồ thị hàm số như hình vẽ bên. Tìm số điểm cực trị của hàm số

A.13
B.11
C.10
D.12
* Đáp án
* Hướng dẫn giải
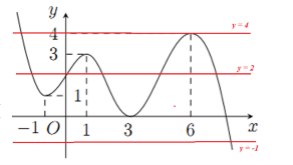
Ta có:
có tất cả: nghiệm
(trong đó, có các nghiệm là nghiệm kép, còn lại là nghiệm đơn)
có 12 nghiệm phân biệt, trong đó, là nghiệm bội 3, còn lại là nghiệm đơn.
Do đó, số điểm cực trị của hàm số là 12.
Đáp án cần chọn là: D
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Cực trị của hàm số !!
Số câu hỏi: 70
Copyright © 2021 HOCTAP247
