Trang chủ Đề thi & kiểm tra Khác Cực trị của hàm số !! Cho hàm số y=f(x) có đạo hàm f′(x) có đồ...

Cho hàm số y=f(x) có đạo hàm f′(x) có đồ thị. Số điểm cực trị của hàm số g(x)=8f(x^3 - 3x + 3)-(x^6-12x^4+16x^3+18x^2-48+1)

Câu hỏi :

Cho hàm số y=fx có đạo hàm f′(x) có đồ thị như hình dưới đây


A.5



B.8


C.7 

D.9

* Đáp án

* Hướng dẫn giải

Ta có:

g(x)=8f(x3−3x+3) −(2x6−12x4+16x3+18x2−48x+1) 

g'(x)=24(x2−1)[f'(x3−3x+3)−12(x3−3x+3+1)]

g'(x)=0

⇔x=±1f'(x3−3x+3)=12(x3−3x+3+1)*

Đặt t=x3−3x+3  phương trình (*) trở thành f't=12t+1 do đó số nghiệm của phương trình là số giao điểm của đồ thị hàm số y=f't và y=12t+1

 

 
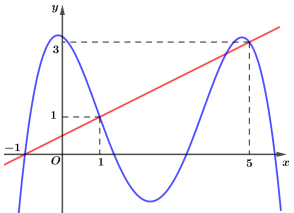
Media VietJack

Dựa vào đồ thị hàm số ta thấy (∗) ⇔t=−1t=1t=5t=t0∈(1;5)

+ Với t=−1⇒x3−3x+3=−1  phương trình này có 1 nghiệm không nguyên.

+ Với  t=1⇒x3−3x+3=1⇔x=1x=−2  trong đó x = 1 là nghiệm bội 2.

+ Với t=5⇒x3−3x+3=5⇔x=2x=−1 trong đó x = −1 là nghiệm bội 2.

+ Với  t=t0∈1;5⇒1<t0<5  ta có phương trình x3−3x+3=t0

Xét hàm số hx=x3−3x+3 ta có:

h'(x)=3x2−3=0⇔x=1x=−1

BBT:

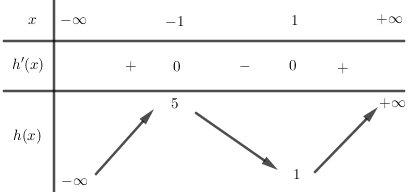
Media VietJack

Từ BBT suy ra phương trình x3−3x+3=t0 có 3 nghiệm phân biệt.

Suy ra phương trình g'x=0  có 8 nghiệm phân biệt và g′(x) đổi dấu qua các nghiệm này 

( x=±1là nghiệm bội ba) nên hàm số g(x) có 8 điểm cực trị.

Đáp án cần chọn là: B

Câu hỏi trên thuộc đề trắc nghiệm dưới đây !

Cực trị của hàm số !!

Số câu hỏi: 70

Khác

Home
Tiểu học Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 Hóa học Tài liệu Đề thi & kiểm tra Câu hỏi hoctapsgk.com Nghe truyện audio Đọc truyện chữ Công thức nấu ăn

Copyright © 2021 HOCTAP247