Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P):2x-y-2z-2=0
Câu hỏi :
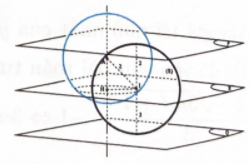
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng và mặt phẳng song song với nhau. Biết A(1;2;1) là điểm nằm giữa hai mặt phẳng (P) và (Q). Gọi (S) là mặt cầu qua A và tiếp xúc với cả hai mặt phẳng (P) và (Q). Biết rằng khi (S) thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính r của đường tròn đó
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng và mặt phẳng song song với nhau. Biết A(1;2;1) là điểm nằm giữa hai mặt phẳng (P) và (Q). Gọi (S) là mặt cầu qua A và tiếp xúc với cả hai mặt phẳng (P) và (Q). Biết rằng khi (S) thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính r của đường tròn đó
A.
B.
C.
* Đáp án
* Hướng dẫn giải
Bước 1: Tính
Ta thấy M(1;0;0) là một điểm thuộc (P)
Vì nên
Bước 2: Giả sử I(a;b;c) là tâm của (S). Chứng minh I luôn thuộc mặt phẳng (R)
Giả sử I(a;b;c) là tâm của (S). Vì (S) tiếp xúc với cả (P) và (Q) nên bán kính mặt cầu (S) là
Do đó IA=2 nên I luôn thuộc mặt cầu (T) tâm A, bán kính 2
Ngoài ra,
Do đó, I luôn thuộc mặt phẳng
Bước 3: Gọi H là hình chiếu vuông góc của A lên (R).Tính HI và tính bán kính r
Gọi H là hình chiếu vuông góc của A lên (R). Vì A,
Ta có
Mà ,do đó vuông tại H nên
Vậy I luôn thuộc đường tròn tâm H, nằm trên mặt phẳng (R), bán kính
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Mặt cầu và mặt phẳng !!
Copyright © 2021 HOCTAP247
