Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ bên, một hàm số g(x) xác định theo f(x)
Câu hỏi :
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ bên, một hàm số g(x) xác định theo f(x) có đạo hàm . Tìm tất cả các giá trị thực của tham số mm để hàm số g(x) có duy nhất một cực trị.
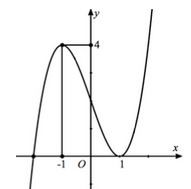
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ bên, một hàm số g(x) xác định theo f(x) có đạo hàm . Tìm tất cả các giá trị thực của tham số mm để hàm số g(x) có duy nhất một cực trị.

A.−4 < m < 0
B. hoặc
C.m > 0 hoặc m < −4
D.
* Đáp án
* Hướng dẫn giải
Hàm số g(x) có duy nhất một cực trị có đúng một nghiệm thỏa mãn g′(x) đổi dấu qua nghiệm đó.
Theo đề bài ta có:
=>Số nghiệm của pt là số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = −m.
Quan sát đồ thị ta thấy đường thẳng y = −m cắt đồ thị hàm số y = f(x)) tại một điểm duy nhất
Ngoài ra, với m = 0 hoặc m = −4 thì đồ thị hàm số có hai điểm chung với đường thẳng nhưng một điểm là điểm tiếp xúc nên phương trình có hai nghiệm phân biệt, trong đó có một nghiệm kép và một nghiệm đơn.
Nên trong trường hợp này, hàm số vẫn chỉ có một cực trị.
Vậy hoặc .
Đáp án cần chọn là: B
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài toán cực trị có tham số đối với một số hàm số cơ bản !!
Copyright © 2021 HOCTAP247
