Trang chủ
Đề thi & kiểm tra
Khác
Bài toán cực trị có tham số đối với một số hàm số cơ bản !!
Cho hàm số y=(x-m)^3-3x+m^2 có đồ thị là (Cm) với...
Cho hàm số y=(x-m)^3-3x+m^2 có đồ thị là (Cm) với m là tham số thực. Biết điểm M(a;b)
Câu hỏi :
Cho hàm số có đồ thị là (Cm) với m là tham số thực. Biết điểm M(a;b) là điểm cực đại của (Cm) ứng với một giá trị m thích hợp, đồng thời là điểm cực tiểu của (Cm) ứng với một giá trị khác của m. Tổng bằng
Cho hàm số có đồ thị là (Cm) với m là tham số thực. Biết điểm M(a;b) là điểm cực đại của (Cm) ứng với một giá trị m thích hợp, đồng thời là điểm cực tiểu của (Cm) ứng với một giá trị khác của m. Tổng bằng
A.504.
B.−504.
C.12504.
D.5004.
* Đáp án
* Hướng dẫn giải
Vì điểm M(a;b) thuộc đồ thị (Cm) nên ta có:
Xét
Bảng biến thiên
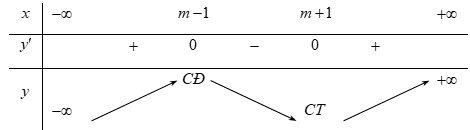
Dựa vào bảng biến thiên, ta có:
Nếu là giá trị của tham số m để đồ thị hàm số nhận điểm M(a;b) là điểm cực đại thì . Nếu là giá trị của tham số m để đồ thị hàm số nhận điểm M(a;b) là điểm cực tiểu thì
Do đó
Mà phải thỏa mãn (1)nên ta có:
Vậy
Đáp án cần chọn là: A
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài toán cực trị có tham số đối với một số hàm số cơ bản !!
Số câu hỏi: 57
Copyright © 2021 HOCTAP247
