Trang chủ
Đề thi & kiểm tra
Lớp 7
Toán học
Trắc nghiệm Toán 7 Bài 8. Tính chất ba đường cao của tam giác có đáp án !!
Cho tam giác ABC nhọn có ba đường cao AM,...
Cho tam giác ABC nhọn có ba đường cao AM, BN, CP. Biết AM = BN = CP.
Câu hỏi :
Cho tam giác ABC nhọn có ba đường cao AM, BN, CP. Biết AM = BN = CP. Khi đó tam giác ABC là:
Cho tam giác ABC nhọn có ba đường cao AM, BN, CP. Biết AM = BN = CP. Khi đó tam giác ABC là:
A. Tam giác vuông;
B. Tam giác vuông cân;
C. Tam giác đều;
D. Tam giác cân.
* Đáp án
* Hướng dẫn giải
Hướng dẫn giải
Đáp án đúng là: C
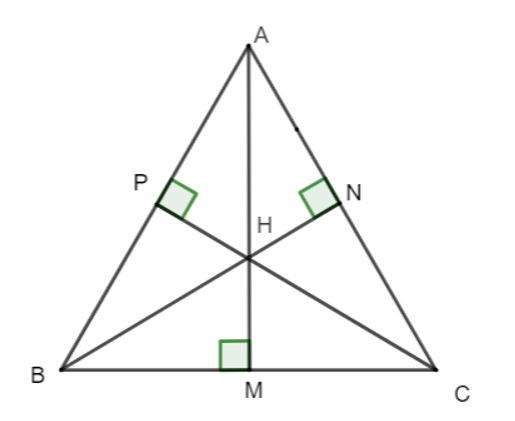
Gọi H là giao điểm của ba đường cao.
Ta có: + = 90°;
+ = 90°;
= (hai góc đối đỉnh).
Do đó = .
Xét ∆ABM vuông tại M và ∆CBP vuông tại P ta có:
= (cmt).
AM = CP (gt).
Do đó ∆ABM = ∆CBP (cạnh góc vuông - góc nhọn).
Suy ra AB = BC (hai cạnh tương ứng) (1)
Chứng minh tương tự ta được ∆BNC = ∆AMC (cạnh góc vuông - góc nhọn)
Suy ra BC = AC (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra AB = BC = AC.
Vậy ∆ABC là tam giác đều.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Trắc nghiệm Toán 7 Bài 8. Tính chất ba đường cao của tam giác có đáp án !!
Số câu hỏi: 15
Copyright © 2021 HOCTAP247
