Cho hình chóp S.ABC có SA vuông góc (ABC); AC = b, AB = c, góc BAC = alpha . Gọi B′,C′ lần lượt là hình chiếu

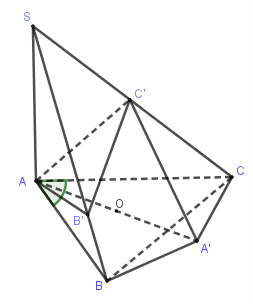
Gọi AA′  là đường kính của đường tròn ngoại tiếp tam giác ABC

$AC\perp A^{\text{'}}C;AB\perp A^{\text{'}}B$

Ta chứng minh  $A{C}^{\text{'}}\perp A^{\text{'}}{C}^{\text{'}}$

Mà $A{C}^{\text{'}}\perp SC\Rightarrow A{C}^{\text{'}}\perp A^{\text{'}}{C}^{\text{'}}$

Tương tự $A{B}^{\text{'}}\perp A^{\text{'}}{B}^{\text{'}}$

Như vậy B,C,C′,B′ cùng nhìn AA′  bằng 1  góc vuông nên A,B,C,B′,C′ cùng thuộc 1  mặt cầu có đường kính là AA′  và cũng đồng thời là đường kính của đường tròn ngoại tiếp tam giác ABC.

Tính $BC=\sqrt{b^2+c^2-2b\cos \alpha }$

Trong tam giác $ABC:\frac{BC}{\sin A}=2R\Rightarrow R=\frac{\sqrt{b^2+c^2-2bc\cos \alpha }}{2\sin \alpha }$
Đáp án cần chọn là: C