Trang chủ
Đề thi & kiểm tra
Khác
Mặt cầu ngoại tiếp, nội tiếp !!
Cho tứ diện ABCD có AB = a;AC = BC...
Cho tứ diện ABCD có AB = a;AC = BC = AD = BD = a căn bậc hai của 3/2. Gọi M,N là trung điểm của AB,CD.
Câu hỏi :
Cho tứ diện ABCD có AB = a;AC = BC = AD = BD =. Gọi M,N là trung điểm của AB,CD. Góc giữa hai mặt phẳng (ABD);(ABC) là . Tính biết mặt cầu đường kính MN tiếp xúc với cạnh AD.
Cho tứ diện ABCD có AB = a;AC = BC = AD = BD =. Gọi M,N là trung điểm của AB,CD. Góc giữa hai mặt phẳng (ABD);(ABC) là . Tính biết mặt cầu đường kính MN tiếp xúc với cạnh AD.
A.
B.
C.
D.
* Đáp án
* Hướng dẫn giải
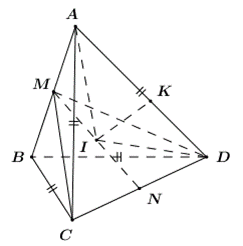
Xét các tam giác ACB, ADB lần lượt cân tại C và D nên
Ta có :
Tam giác ACM vuông tại M nên theo Pitago ta có :
Tương tự
Gọi K là hình chiếu của I lên AD ta có :
Mặt cầu đường kính MN tiếp xúc với AD nên .
Xét tam giác AMI và AKI có :
Do đó (cạnh huyền – cạnh góc vuông) (cạnh tương ứng).
Tương tự : (cạnh huyền – cạnh góc vuông)
Áp dụng định lý cô sin trong tam giác MCD có :
Đáp án cần chọn là: B
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Mặt cầu ngoại tiếp, nội tiếp !!
Số câu hỏi: 33
Copyright © 2021 HOCTAP247
