Cho khối lăng trụ tam giác đều ABC.A′B′C′. Các mặt phẳng (ABC′) và (A′B′C) chia khối lăng trụ
Câu hỏi :
Cho khối lăng trụ tam giác đều ABC.A′B′C′. Các mặt phẳng (ABC′) và (A′B′C) chia khối lăng trụ đã cho thành 4 khối đa diện. Kí hiệu H1, H2 lần lượt là khối có thể tích lớn nhất và nhỏ nhất trong bốn khối trên. Giá trị của bằng
Cho khối lăng trụ tam giác đều ABC.A′B′C′. Các mặt phẳng (ABC′) và (A′B′C) chia khối lăng trụ đã cho thành 4 khối đa diện. Kí hiệu H1, H2 lần lượt là khối có thể tích lớn nhất và nhỏ nhất trong bốn khối trên. Giá trị của bằng
A.4
B.2
C.5
* Đáp án
* Hướng dẫn giải
Bước 1:
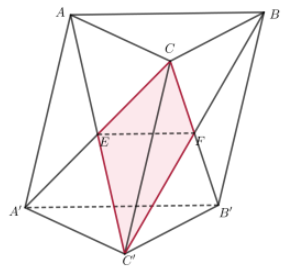
Gọi E là giao điểm của AC và AC’ và F là giao điểm của BC’ và B’C’
Khi đó (ABC’) và (A’B’C) chia khối lăng trụ tam giác đều ABC.A’B’C’ thành 4 khối đa diện: CEFC’;FEA’B’C’;FEABC và FEABB’A’
Gọi V là thể tích của khối lăng trụ tam giác đều ABC.A’B’C’.
Bước 2: Tính thể tích của và theo thể tích của
Ta có
và
Mặt khác
Do đó có thể tích lớn nhất là khối đa diện FEABB’A’; có thể tích nhỏ nhất là khối đa diện CEFC’ và
Đáp án cần chọn là: C
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Thể tích khối hộp !!
Copyright © 2021 HOCTAP247
