Trên cạnh AB lấy điểm D (D nằm giữa N và B, và trên tia đối tia CA lấy điểm E sao c

Chứng minh $\Delta DFC=\Delta CED\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}( g-c-g)}$

Nên $FD=CE$ và $\widehat{DFC}=\widehat{CED}$

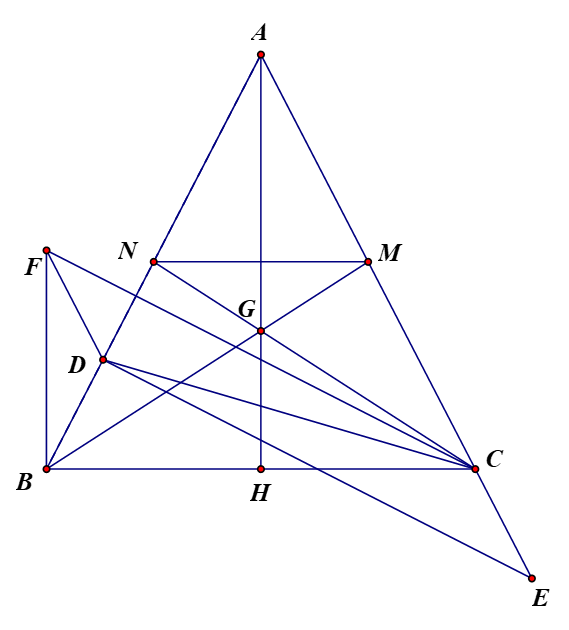
Chứng minh tam giác DFB cân tại D (vì $DF=DB=CE$ )

Ta có $\widehat{BFC}=\widehat{BFD}+\widehat{DFC}$ và $\widehat{FBC}=\widehat{FBD}+\widehat{DBC}$

Mà $\widehat{BFD}=\widehat{FBD}$ (góc đáy tam giác cân)

Ta có $\widehat{ACD}>\widehat{CED}$ (góc ngoài tam giác)

Mà $\widehat{ACD}<\widehat{ACB}=\widehat{ABC}$ nên $\widehat{DFC}<\widehat{DBC}$

Cho nên $\widehat{BFC}<\widehat{FBC}$.

Vậy $FC>BC$ (quan hệ góc và cạnh đối diện)