Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho

Câu hỏi :

Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM = ON, OA > OM. Chứng minh rằng:

a) ∆OAN = ∆OBM;

* Đáp án

* Hướng dẫn giải

GT	$\widehat{xOy}$; A, M ∈ Ox; B, N ∈ Oy; OA = OB, OM = ON, OA > OM
KL	a) ∆OAN = ∆OBM; b) ∆AMN = ∆BNM.

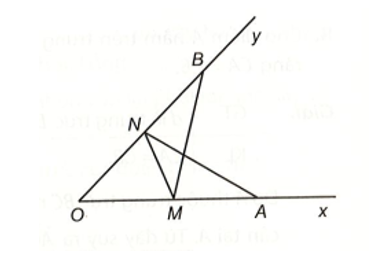
a) Xét hai tam giác OAN và OBM có:

OA = OB (theo giả thiết).

$\widehat{NOA}=\widehat{xOy}=\widehat{MOB}$

ON = OM (theo giả thiết).

Vậy ∆OAN = ∆OBM (c – g – c).