Trang chủ
Đề thi & kiểm tra
Lớp 7
Toán học
Sách bài tập Toán 7 Tập 1 !!
Cho tam giác ABC cân tại A. Kẻ BD vuông...
Cho tam giác ABC cân tại A. Kẻ BD vuông góc với AC, kẻ CE
Câu hỏi :
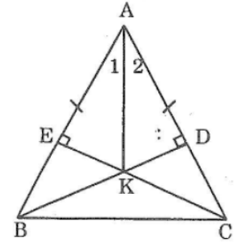
Cho tam giác ABC cân tại A. Kẻ BD vuông góc với AC, kẻ CE vuông góc với AB. Gọi K là giao điểm của BD và CE. Chứng minh rằng AK là tia phân giác của góc A.
* Đáp án
* Hướng dẫn giải
Xét ΔADB vuông tại D và ΔAEC vuông tại E, ta có:
AB = AC (giả thiết)
∠(BAC) chung
⇒ ΔADB = ΔAEC (cạnh huyền, góc nhọn)
⇒ AD = AE (hai cạnh tương ứng)
Xét ΔADK vuông tại D và ΔAEK vuông tại E có:
AD = AE (chứng minh trên)
AK cạnh chung
⇒ ΔADK = ΔAEK (cạnh huyền, cạnh góc vuông)
⇒ ∠(DAK) = ∠(EAK) (hai góc tương ứng)
Vậy AK là tia phân giác của góc BAC.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Sách bài tập Toán 7 Tập 1 !!
Số câu hỏi: 795
Copyright © 2021 HOCTAP247