Đặt một hiệu điện thế \(U\) vào hai đầu một đoạn mạch có sơ đồ như trên hình vẽ.
Câu hỏi :
Đặt một hiệu điện thế \(U\) vào hai đầu một đoạn mạch có sơ đồ như trên hình vẽ. Khi đóng công tắc K vào vị trí 1 thì ampe kế có số chỉ \({I_1} = I\), khi chuyển công tắc này sang vị trí số 2 thì ampe kế có số chỉ là \({I_2} = \frac{I}{3}\), còn khi chuyển K sang vị trí 3 thì ampe kế có số chỉ \({I_3} = \frac{I}{8}\). Cho biết \({R_1} = 3\Omega \) , hãy tính \({R_2};{R_3}\) ?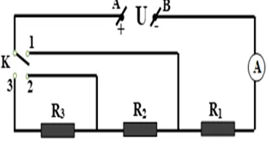
A. \({R_2} = 12\Omega ;{R_3} = 15\Omega \)
B. \({R_2} = 2\Omega ;{R_3} = 5\Omega \)
C. \({R_2} = 6\Omega ;{R_3} = 9\Omega \)
D. \({R_2} = 6\Omega ;{R_3} = 15\Omega \)
* Đáp án
D
* Hướng dẫn giải
+ Khi K ở vị trí 1: Mạch điện chỉ có \({R_1}\) nối tiếp với ampe kế. Do vậy số chỉ của ampe kế khi này là:
\({I_1} = \frac{U}{{{R_1}}} = \frac{U}{3} = I{\mkern 1mu} \,\,{\mkern 1mu} {\mkern 1mu} \left( 1 \right)\)
+ Khi K ở vị trí số 2: Mạch điện có \({R_2}\) nối tiếp \({R_1}\) và nối tiếp với ampe kế.
Do vậy số chỉ của ampe kế khi này là: \({I_2} = \frac{U}{{{R_1} + {R_2}}} = \frac{U}{{3 + {R_2}}} = \frac{I}{3}{\mkern 1mu} \,\,{\mkern 1mu} \left( 2 \right)\)
+ Khi K ở vị trí số 3: Mạch điện gồm 3 điện trở \({R_1},{R_2},{R_3}\) ghép nối tiếp và nối tiếp với ampe kế.
Do vậy số chỉ của ampe kế khi này là: \({I_3} = \frac{U}{{{R_1} + {R_2} + {R_3}}} = \frac{U}{{3 + {R_2} + {R_3}}} = \frac{I}{8}\,\,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( 3 \right)\)
Từ (1) và (2) ta có: \({I_1} = 3{I_2} \Leftrightarrow \frac{U}{3} = 3.\frac{U}{{3 + {R_2}}} \Rightarrow {R_2} = 6\Omega \)
Từ (1) và (3) ta có: \({I_1} = 8{I_3} \Leftrightarrow \frac{U}{3} = 8.\frac{U}{{3 + 6 + {R_3}}} \Rightarrow {R_3} = 15\Omega \)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề ôn tập hè môn Vật Lý 9 năm 2021 Trường THCS Lê Văn Việt
Copyright © 2021 HOCTAP247
