Trang chủ
Lớp 6
Toán Lớp 6 SGK Cũ
Bài 6. Tia phân giác của góc
Giải bài 37 trang 87 - Sách giáo khoa Toán 6 tập 2
Giải bài 37 trang 87 - Sách giáo khoa Toán 6 tập 2
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
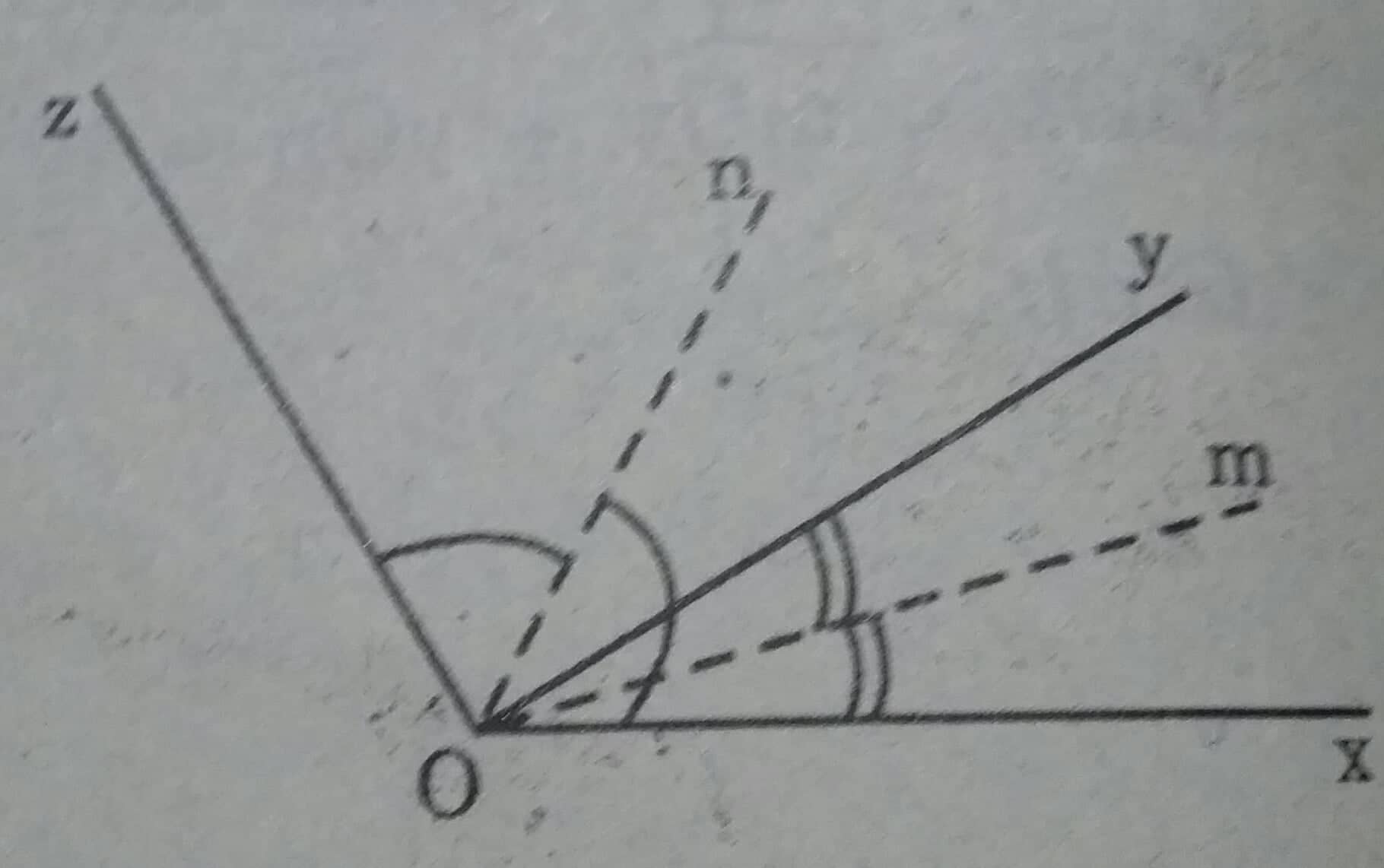
Cho hai tia Oy, Oz cùng nằm trên một nửa mặt phẳng có bờ chứa tia Ox. Biết góc xOy = \(30^0\), góc xOz = \(120^0\).
Hướng dẫn giải
Hai tia Oy, Oz cùng nằm trên một nửa mặt phẳng có bờ chứa tia Ox.
Mà \(\widehat{xOy}< \widehat{xOz}( 30^0 < 120^0)\)
Nên tia Ox nằm giữ hai tia Ox, Oz.
Do đó \(\widehat{xOy}+ \widehat{yOz}= \widehat{xOz}\)
\(\widehat{yOz}= \widehat{xOz}- \widehat{xOy}= 120^0 - 30^0 = 90^0\)
Tia Om là tia phân giác của góc \(\widehat{xOz}\) nên:
\(\widehat{xOn}= \widehat{xOz}:2= 120^0 : 2= 60^0\)
Tia Om nằm giữa hai tia \(Ox, On ( \widehat{xOm}< \widehat{xOn}) \) nên
\( \widehat{xOm}+ \widehat{mOn}= \widehat{xOn}\)
\(\widehat{mOn}= \widehat{xOn}- \widehat{xOm}= 60^0 - 15^0 = 45^0\)
Copyright © 2021 HOCTAP247
