Giải bài 55 trang 80 - Sách giáo khoa Toán 7 tập 2

Đề bài

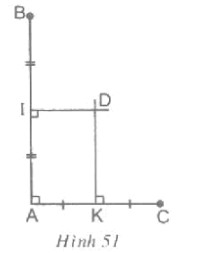
Cho hình 51: Chứng minh ba điểm B, C, D thẳng hàng.

Hướng dẫn giải

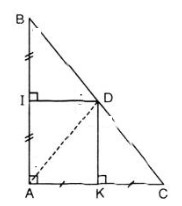
Nối BD và CD.

Từ hình vẽ ta có DK là đường trung trực của AC \(\Rightarrow DA = DC.\)

Từ hình vẽ ta có DI là đường trung trực của AB \(\Rightarrow DA = DB.\)

Xét ΔADK và ΔCDK có:

\(   AD = CD\,\ (cmt)\)

    DK chung

    \(AK = KC\,\ (gt)\)

\(\Rightarrow ΔADK = ΔCDK\,\ (c-c-c)\)

\(\Rightarrow \widehat{ADK}= \widehat{CDK}\)

hay DK là phân giác \(\widehat{ADC}\)

\(\Rightarrow \widehat{ADK} = \dfrac{1}{2}.\widehat{ADC}\)

Tương tự chứng minh trên, ta có: \(∆ADI = ∆BDI (c-c-c)\)

\(\Rightarrow \widehat{ADI}= \widehat{BDI}\)

\(\Rightarrow DI \) là phân giác \(\widehat{ADB}\)

\(\Rightarrow \widehat{ADI}= \dfrac{1}{2}.\widehat{ADB}\)

Vì AC // DI (cùng vuông góc với AB) mà DK ⊥ AC 

\(\Rightarrow\) DK ⊥ DI

hay \(\widehat{ADK}+ \widehat{ADI}= 90^0\)

Do đó \(\dfrac{1}{2}.\widehat{ADC}+ \dfrac{1}{2}.\widehat{ADB} = 90^0\)

\(\Rightarrow \widehat{ADC}+ \widehat{ADB} = 180^0\)

Vậy B,C,D thẳng hàng.