Giải bài 3 trang 115 - Sách giáo khoa Toán 8 tập 1

Đề bài

Cho hình thoi ABCD có góc ∠A = 60\(^0\). Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng đa giác EBFGDH là lục giác đều.

Hướng dẫn giải

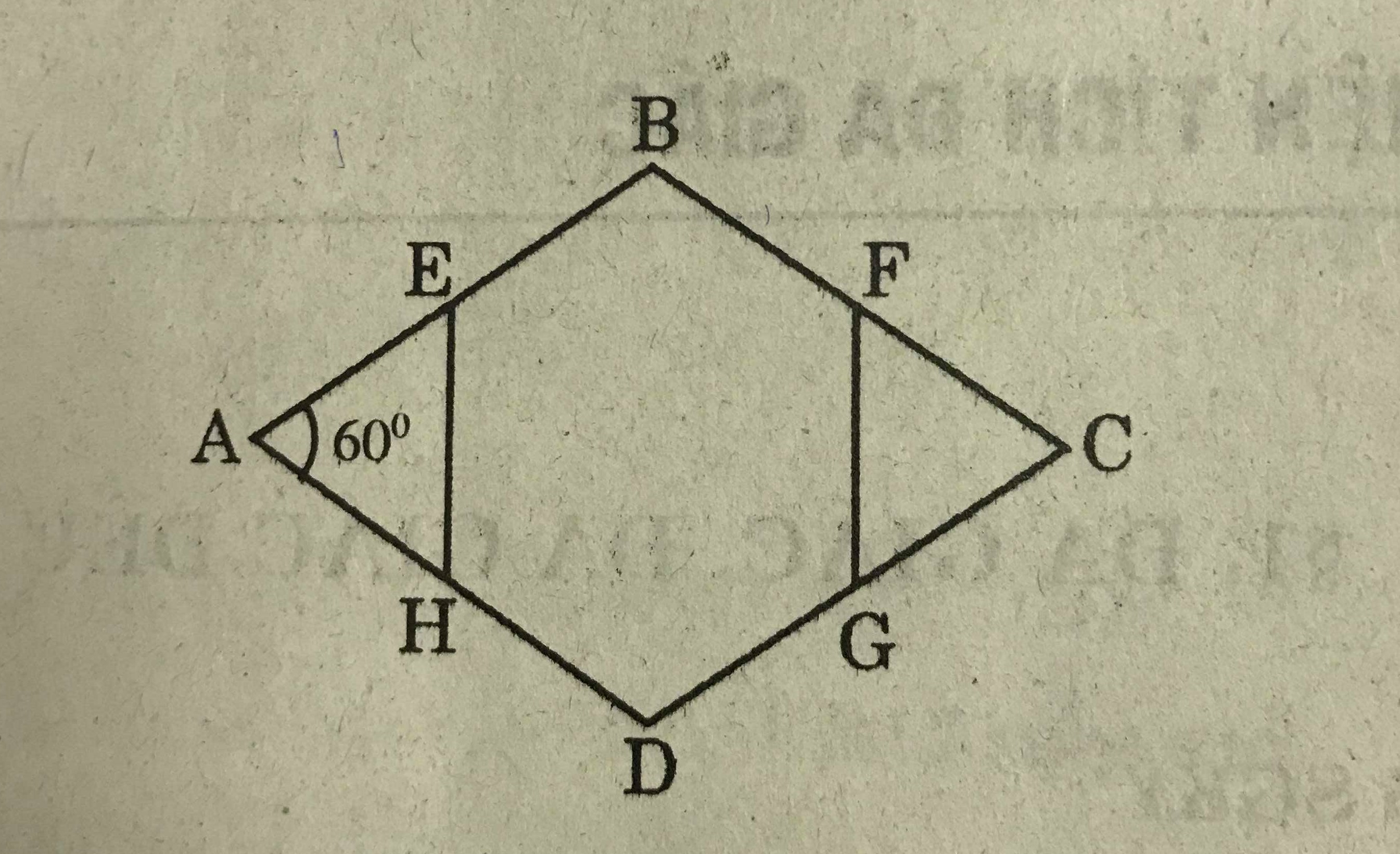
Góc A = \(60^0\) và AB = AD nên \(\triangle\)ABD đều.

=> BD = AB = AD.

EH là đường trung bình của \(\triangle\)ABD.

=> EH = \(\dfrac{BD}{2}\)

FG là đường trung bình của \(\triangle\)BCD.

=> FG = \(\dfrac{BD}{2}\)

Lại có :

BE = \(\dfrac{AB}{2}\)                         BF = \(\dfrac{BC}{2}\)

DH = \(\dfrac{AD}{2}\)                        DG = \(\dfrac{DC}{2}\) (gt)

Do đó : BE = EH = HD = DG = GF = FB                (1)

\(\triangle\)AEH có : \(\widehat{A}=60^0\) và AE = AH nên là tam giác đều.

=> \(\widehat{AEH}=60^0\) => \(\widehat{BEH}=120^0\)

Tương tự : \(\widehat{EHD}=120^0,\widehat{DGF}=120^0,\widehat{BFG}=120^0\)

Mặt khác : \(\widehat{B}=60^0,\widehat{D}=120^0\)

Do đó : \(\widehat{E}=\widehat{B}=\widehat{F}=\widehat{G}=\widehat{D}=\widehat{H}=120^0\)         (2)

Từ (1) và (2) suy ra : Lục giác EBFGDH là lục giác đều.