Trang chủ
Lớp 9
Toán Lớp 9 SGK Cũ
Bài 2. Tỉ số lượng giác của góc nhọn
Bài 16 trang 77 SGK Toán 9 tập 1
Bài 16 trang 77 SGK Toán 9 tập 1
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho tam giác vuông có một góc bằng \(60^{\circ}\) và cạnh huyền có độ dài bằng \(8\). Hãy tìm độ dài của cạnh đối diện góc \(60^{\circ}\).
Hướng dẫn giải
Dựa vào định nghĩa tỷ số lượng giác của góc nhọn:
\(\sin \alpha =\dfrac{cạnh\ đối}{cạnh \ huyền} \)
\(\Rightarrow {cạnh\ đối} = \sin \alpha. {cạnh\ huyền}.\)
Lời giải chi tiết
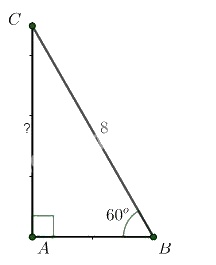
Xét \(\Delta{ABC}\) vuông tại \(A\), theo định nghĩa tỷ số lượng giác của góc nhọn, ta có:
\(\sin B = \dfrac{AC}{BC} \Leftrightarrow \sin 60^o = \dfrac{AC}{8}\)
\(\Leftrightarrow AC =8. \sin 60^o=8.\dfrac{\sqrt 3}{2}=4\sqrt 3.\)
Vậy cạnh đối diện với góc \(60^o\) là \(AC=4\sqrt 3\).
Copyright © 2021 HOCTAP247
