Giải bài 14 trang 77 - Sách giáo khoa Toán 9 tập 1
Tóm tắt bài
Đề bài
Sử dụng định nghĩa các tỉ số lượng giác của một góc nhọn để chứng minh rằng. Với góc nhọn α tùy ý, ta có:
Hướng dẫn giải
Hướng dẫn:
- Các tỉ số lượng giác của góc nhọn \(\alpha\) trong tam giác vuông ABC (vuông tại A):
\(sin \alpha = \frac{AC}{BC}\) ; \(cos \alpha =\frac{AB}{BC}\)
\(tg \alpha = \frac{AC}{AB}\); \(cotg \alpha =\frac{AB}{AC}\)
- Biến đổi vế trái của đẳng thức bằng vế phải hoặc biến đổi vế phải của đẳng thức bằng vế trái.
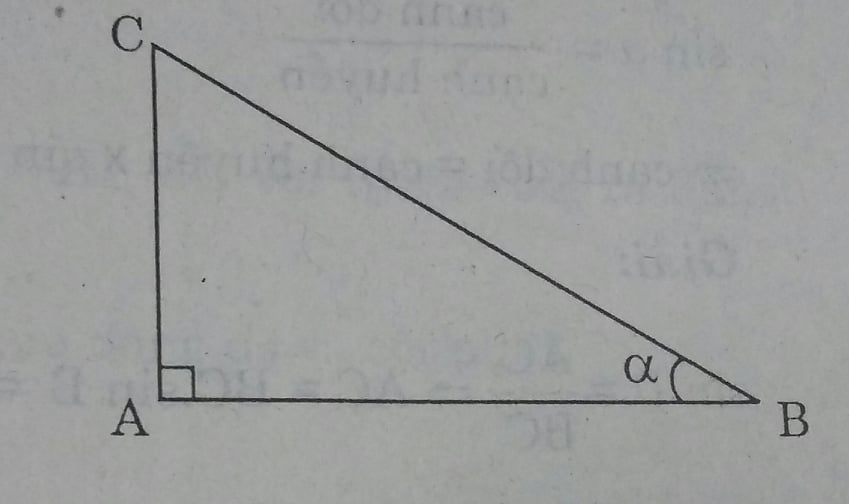
Giải:
Ta có:
\( \frac {sin \alpha }{cos \alpha}=\frac{AC}{BC}:\frac{AB}{BC}=\frac{AC}{BC}.\frac{BC}{AB}=\frac{AC}{AB}=tg \alpha\)
\( \frac {cos \alpha }{sin \alpha}=\frac{AB}{BC}:\frac{AC}{BC}=\frac{AB}{BC}.\frac{BC}{AC}=\frac{AB}{AC}=cotg \alpha\)
\(tag\alpha.cotg\alpha = \frac{AC}{AB}.\frac{AB}{AC}=1\)
b) \(sin ^2 \alpha+ cos^2 \alpha = (\frac{AC}{BC})^2+ (\frac{AB}{BC})^2= \frac{AC^2+AB^2}{BC^2}=\frac{BC^2}{BC^2}=1\)
Copyright © 2021 HOCTAP247
